Markov switching dynamic regression models

This notebook provides an example of the use of Markov switching models in statsmodels to estimate dynamic regression models with changes in regime. It follows the examples in the Stata Markov switching documentation, which can be found at http://www.stata.com/manuals14/tsmswitch.pdf.

%matplotlib inline

import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt

# NBER recessions
from pandas_datareader.data import DataReader
from datetime import datetime
usrec = DataReader('USREC', 'fred', start=datetime(1947, 1, 1), end=datetime(2013, 4, 1))

Federal funds rate with switching intercept

The first example models the federal funds rate as noise around a constant intercept, but where the intercept changes during different regimes. The model is simply:

\[r_t = \mu_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]

where \(S_t \in \{0, 1\}\), and the regime transitions according to

\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]

We will estimate the parameters of this model by maximum likelihood: \(p_{00}, p_{10}, \mu_0, \mu_1, \sigma^2\).

The data used in this example can be found at https://www.stata-press.com/data/r14/usmacro.

# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import fedfunds
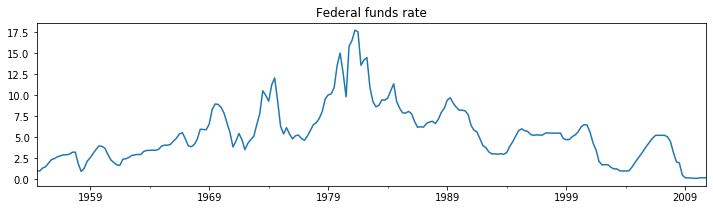
dta_fedfunds = pd.Series(fedfunds, index=pd.date_range('1954-07-01', '2010-10-01', freq='QS'))

# Plot the data
dta_fedfunds.plot(title='Federal funds rate', figsize=(12,3))

# Fit the model
# (a switching mean is the default of the MarkovRegession model)
mod_fedfunds = sm.tsa.MarkovRegression(dta_fedfunds, k_regimes=2)
res_fedfunds = mod_fedfunds.fit()

res_fedfunds.summary()

Markov Switching Model Results

Dep. Variable:	y	No. Observations:	226
Model:	MarkovRegression	Log Likelihood	-508.636
Date:	Tue, 17 Dec 2019	AIC	1027.272
Time:	23:40:27	BIC	1044.375
Sample:	07-01-1954	HQIC	1034.174
	- 10-01-2010
Covariance Type:	approx

Regime 0 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	3.7088	0.177	20.988	0.000	3.362	4.055

Regime 1 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	9.5568	0.300	31.857	0.000	8.969	10.145

Non-switching parameters

	coef	std err	z	P>|z|	[0.025	0.975]
sigma2	4.4418	0.425	10.447	0.000	3.608	5.275

Regime transition parameters

	coef	std err	z	P>|z|	[0.025	0.975]
p[0->0]	0.9821	0.010	94.443	0.000	0.962	1.002
p[1->0]	0.0504	0.027	1.876	0.061	-0.002	0.103

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

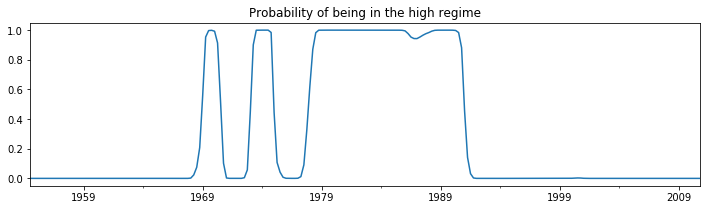
From the summary output, the mean federal funds rate in the first regime (the “low regime”) is estimated to be \(3.7\) whereas in the “high regime” it is \(9.6\). Below we plot the smoothed probabilities of being in the high regime. The model suggests that the 1980’s was a time-period in which a high federal funds rate existed.

res_fedfunds.smoothed_marginal_probabilities[1].plot(
    title='Probability of being in the high regime', figsize=(12,3));

From the estimated transition matrix we can calculate the expected duration of a low regime versus a high regime.

print(res_fedfunds.expected_durations)

[55.85400626 19.85506546]

A low regime is expected to persist for about fourteen years, whereas the high regime is expected to persist for only about five years.

Federal funds rate with switching intercept and lagged dependent variable

The second example augments the previous model to include the lagged value of the federal funds rate.

\[r_t = \mu_{S_t} + r_{t-1} \beta_{S_t} + \varepsilon_t \qquad \varepsilon_t \sim N(0, \sigma^2)\]

where \(S_t \in \{0, 1\}\), and the regime transitions according to

\[\begin{split} P(S_t = s_t | S_{t-1} = s_{t-1}) = \begin{bmatrix} p_{00} & p_{10} \\ 1 - p_{00} & 1 - p_{10} \end{bmatrix}\end{split}\]

We will estimate the parameters of this model by maximum likelihood: \(p_{00}, p_{10}, \mu_0, \mu_1, \beta_0, \beta_1, \sigma^2\).

# Fit the model
mod_fedfunds2 = sm.tsa.MarkovRegression(
    dta_fedfunds.iloc[1:], k_regimes=2, exog=dta_fedfunds.iloc[:-1])
res_fedfunds2 = mod_fedfunds2.fit()

res_fedfunds2.summary()

Markov Switching Model Results

Dep. Variable:	y	No. Observations:	225
Model:	MarkovRegression	Log Likelihood	-264.711
Date:	Tue, 17 Dec 2019	AIC	543.421
Time:	23:40:28	BIC	567.334
Sample:	10-01-1954	HQIC	553.073
	- 10-01-2010
Covariance Type:	approx

Regime 0 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.7245	0.289	2.510	0.012	0.159	1.290
x1	0.7631	0.034	22.629	0.000	0.697	0.829

Regime 1 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0989	0.118	-0.835	0.404	-0.331	0.133
x1	1.0612	0.019	57.351	0.000	1.025	1.097

Non-switching parameters

	coef	std err	z	P>|z|	[0.025	0.975]
sigma2	0.4783	0.050	9.642	0.000	0.381	0.576

Regime transition parameters

	coef	std err	z	P>|z|	[0.025	0.975]
p[0->0]	0.6378	0.120	5.304	0.000	0.402	0.874
p[1->0]	0.1306	0.050	2.634	0.008	0.033	0.228

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

There are several things to notice from the summary output:

1. The information criteria have decreased substantially, indicating that this model has a better fit than the previous model.

2. The interpretation of the regimes, in terms of the intercept, have switched. Now the first regime has the higher intercept and the second regime has a lower intercept.

Examining the smoothed probabilities of the high regime state, we now see quite a bit more variability.

res_fedfunds2.smoothed_marginal_probabilities[0].plot(
    title='Probability of being in the high regime', figsize=(12,3));

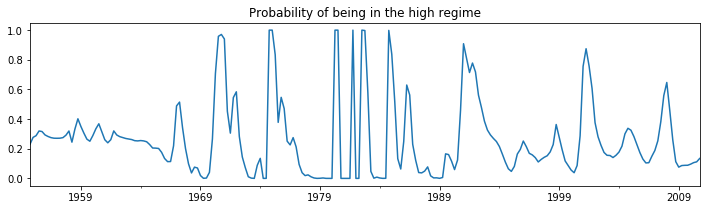
Finally, the expected durations of each regime have decreased quite a bit.

print(res_fedfunds2.expected_durations)

[2.76105188 7.65529154]

Taylor rule with 2 or 3 regimes

We now include two additional exogenous variables - a measure of the output gap and a measure of inflation - to estimate a switching Taylor-type rule with both 2 and 3 regimes to see which fits the data better.

Because the models can be often difficult to estimate, for the 3-regime model we employ a search over starting parameters to improve results, specifying 20 random search repetitions.

# Get the additional data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import ogap, inf
dta_ogap = pd.Series(ogap, index=pd.date_range('1954-07-01', '2010-10-01', freq='QS'))
dta_inf = pd.Series(inf, index=pd.date_range('1954-07-01', '2010-10-01', freq='QS'))

exog = pd.concat((dta_fedfunds.shift(), dta_ogap, dta_inf), axis=1).iloc[4:]

# Fit the 2-regime model
mod_fedfunds3 = sm.tsa.MarkovRegression(
    dta_fedfunds.iloc[4:], k_regimes=2, exog=exog)
res_fedfunds3 = mod_fedfunds3.fit()

# Fit the 3-regime model
np.random.seed(12345)
mod_fedfunds4 = sm.tsa.MarkovRegression(
    dta_fedfunds.iloc[4:], k_regimes=3, exog=exog)
res_fedfunds4 = mod_fedfunds4.fit(search_reps=20)

res_fedfunds3.summary()

Markov Switching Model Results

Dep. Variable:	y	No. Observations:	222
Model:	MarkovRegression	Log Likelihood	-229.256
Date:	Tue, 17 Dec 2019	AIC	480.512
Time:	23:40:34	BIC	517.942
Sample:	07-01-1955	HQIC	495.624
	- 10-01-2010
Covariance Type:	approx

Regime 0 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.6555	0.137	4.771	0.000	0.386	0.925
x1	0.8314	0.033	24.951	0.000	0.766	0.897
x2	0.1355	0.029	4.609	0.000	0.078	0.193
x3	-0.0274	0.041	-0.671	0.502	-0.107	0.053

Regime 1 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0945	0.128	-0.739	0.460	-0.345	0.156
x1	0.9293	0.027	34.309	0.000	0.876	0.982
x2	0.0343	0.024	1.429	0.153	-0.013	0.081
x3	0.2125	0.030	7.147	0.000	0.154	0.271

Non-switching parameters

	coef	std err	z	P>|z|	[0.025	0.975]
sigma2	0.3323	0.035	9.526	0.000	0.264	0.401

Regime transition parameters

	coef	std err	z	P>|z|	[0.025	0.975]
p[0->0]	0.7279	0.093	7.828	0.000	0.546	0.910
p[1->0]	0.2115	0.064	3.298	0.001	0.086	0.337

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

res_fedfunds4.summary()

/home/travis/build/statsmodels/statsmodels/statsmodels/base/model.py:1354: RuntimeWarning: invalid value encountered in sqrt
  bse_ = np.sqrt(np.diag(self.cov_params()))
/home/travis/miniconda/envs/statsmodels-test/lib/python3.7/site-packages/scipy/stats/_distn_infrastructure.py:901: RuntimeWarning: invalid value encountered in greater
  return (a < x) & (x < b)
/home/travis/miniconda/envs/statsmodels-test/lib/python3.7/site-packages/scipy/stats/_distn_infrastructure.py:901: RuntimeWarning: invalid value encountered in less
  return (a < x) & (x < b)
/home/travis/miniconda/envs/statsmodels-test/lib/python3.7/site-packages/scipy/stats/_distn_infrastructure.py:1892: RuntimeWarning: invalid value encountered in less_equal
  cond2 = cond0 & (x <= _a)

Markov Switching Model Results

Dep. Variable:	y	No. Observations:	222
Model:	MarkovRegression	Log Likelihood	-180.806
Date:	Tue, 17 Dec 2019	AIC	399.611
Time:	23:40:35	BIC	464.262
Sample:	07-01-1955	HQIC	425.713
	- 10-01-2010
Covariance Type:	approx

Regime 0 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	-1.0250	0.290	-3.531	0.000	-1.594	-0.456
x1	0.3277	0.086	3.812	0.000	0.159	0.496
x2	0.2036	0.049	4.152	0.000	0.107	0.300
x3	1.1381	0.081	13.977	0.000	0.978	1.298

Regime 1 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	-0.0259	0.087	-0.298	0.765	-0.196	0.144
x1	0.9737	0.019	50.265	0.000	0.936	1.012
x2	0.0341	0.017	2.030	0.042	0.001	0.067
x3	0.1215	0.022	5.606	0.000	0.079	0.164

Regime 2 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.7346	0.130	5.632	0.000	0.479	0.990
x1	0.8436	0.024	35.198	0.000	0.797	0.891
x2	0.1633	0.025	6.515	0.000	0.114	0.212
x3	-0.0499	0.027	-1.835	0.067	-0.103	0.003

Non-switching parameters

	coef	std err	z	P>|z|	[0.025	0.975]
sigma2	0.1660	0.018	9.240	0.000	0.131	0.201

Regime transition parameters

	coef	std err	z	P>|z|	[0.025	0.975]
p[0->0]	0.7214	0.117	6.177	0.000	0.493	0.950
p[1->0]	4.001e-08	nan	nan	nan	nan	nan
p[2->0]	0.0783	0.038	2.079	0.038	0.004	0.152
p[0->1]	0.1044	0.095	1.103	0.270	-0.081	0.290
p[1->1]	0.8259	0.054	15.208	0.000	0.719	0.932
p[2->1]	0.2288	0.073	3.150	0.002	0.086	0.371

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

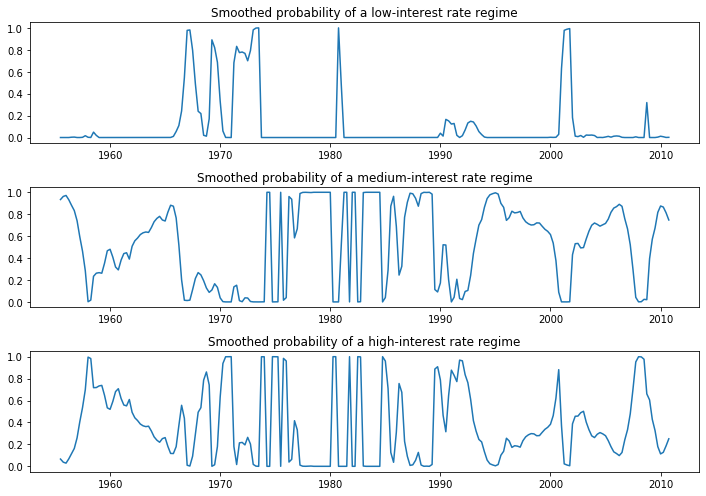
Due to lower information criteria, we might prefer the 3-state model, with an interpretation of low-, medium-, and high-interest rate regimes. The smoothed probabilities of each regime are plotted below.

fig, axes = plt.subplots(3, figsize=(10,7))

ax = axes[0]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[0])
ax.set(title='Smoothed probability of a low-interest rate regime')

ax = axes[1]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[1])
ax.set(title='Smoothed probability of a medium-interest rate regime')

ax = axes[2]
ax.plot(res_fedfunds4.smoothed_marginal_probabilities[2])
ax.set(title='Smoothed probability of a high-interest rate regime')

fig.tight_layout()

Switching variances

We can also accommodate switching variances. In particular, we consider the model

\[y_t = \mu_{S_t} + y_{t-1} \beta_{S_t} + \varepsilon_t \quad \varepsilon_t \sim N(0, \sigma_{S_t}^2)\]

We use maximum likelihood to estimate the parameters of this model: \(p_{00}, p_{10}, \mu_0, \mu_1, \beta_0, \beta_1, \sigma_0^2, \sigma_1^2\).

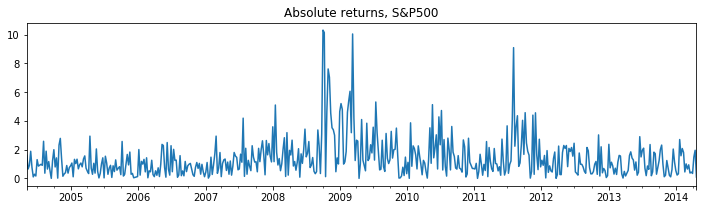
The application is to absolute returns on stocks, where the data can be found at https://www.stata-press.com/data/r14/snp500.

# Get the federal funds rate data
from statsmodels.tsa.regime_switching.tests.test_markov_regression import areturns
dta_areturns = pd.Series(areturns, index=pd.date_range('2004-05-04', '2014-5-03', freq='W'))

# Plot the data
dta_areturns.plot(title='Absolute returns, S&P500', figsize=(12,3))

# Fit the model
mod_areturns = sm.tsa.MarkovRegression(
    dta_areturns.iloc[1:], k_regimes=2, exog=dta_areturns.iloc[:-1], switching_variance=True)
res_areturns = mod_areturns.fit()

res_areturns.summary()

Markov Switching Model Results

Dep. Variable:	y	No. Observations:	520
Model:	MarkovRegression	Log Likelihood	-745.798
Date:	Tue, 17 Dec 2019	AIC	1507.595
Time:	23:40:36	BIC	1541.626
Sample:	05-16-2004	HQIC	1520.926
	- 04-27-2014
Covariance Type:	approx

Regime 0 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	0.7641	0.078	9.761	0.000	0.611	0.918
x1	0.0791	0.030	2.620	0.009	0.020	0.138
sigma2	0.3476	0.061	5.694	0.000	0.228	0.467

Regime 1 parameters

	coef	std err	z	P>|z|	[0.025	0.975]
const	1.9728	0.278	7.086	0.000	1.427	2.518
x1	0.5280	0.086	6.155	0.000	0.360	0.696
sigma2	2.5771	0.405	6.357	0.000	1.783	3.372

Regime transition parameters

	coef	std err	z	P>|z|	[0.025	0.975]
p[0->0]	0.7531	0.063	11.871	0.000	0.629	0.877
p[1->0]	0.6825	0.066	10.301	0.000	0.553	0.812

Warnings:
[1] Covariance matrix calculated using numerical (complex-step) differentiation.

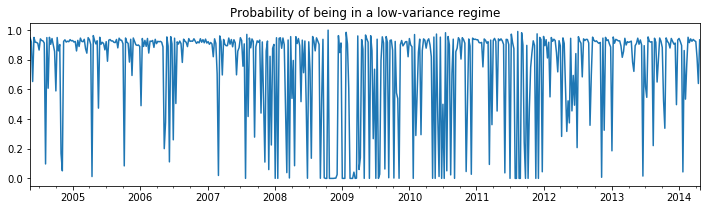
The first regime is a low-variance regime and the second regime is a high-variance regime. Below we plot the probabilities of being in the low-variance regime. Between 2008 and 2012 there does not appear to be a clear indication of one regime guiding the economy.

res_areturns.smoothed_marginal_probabilities[0].plot(
    title='Probability of being in a low-variance regime', figsize=(12,3));