Autoregressive Moving Average (ARMA): Sunspots data¶
[1]:
%matplotlib inline
[2]:
import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
[3]:
from statsmodels.graphics.api import qqplot
Sunspots Data¶
[4]:
print(sm.datasets.sunspots.NOTE)
::
Number of Observations - 309 (Annual 1700 - 2008)
Number of Variables - 1
Variable name definitions::
SUNACTIVITY - Number of sunspots for each year
The data file contains a 'YEAR' variable that is not returned by load.
[5]:
dta = sm.datasets.sunspots.load_pandas().data
[6]:
dta.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))
del dta["YEAR"]
[7]:
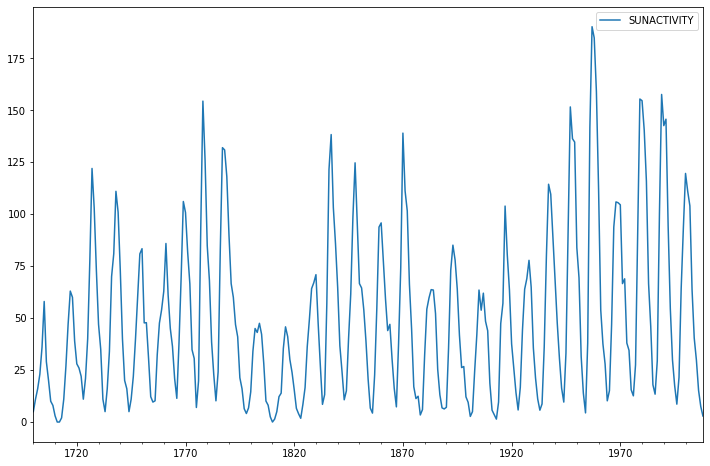
dta.plot(figsize=(12,8));
[8]:
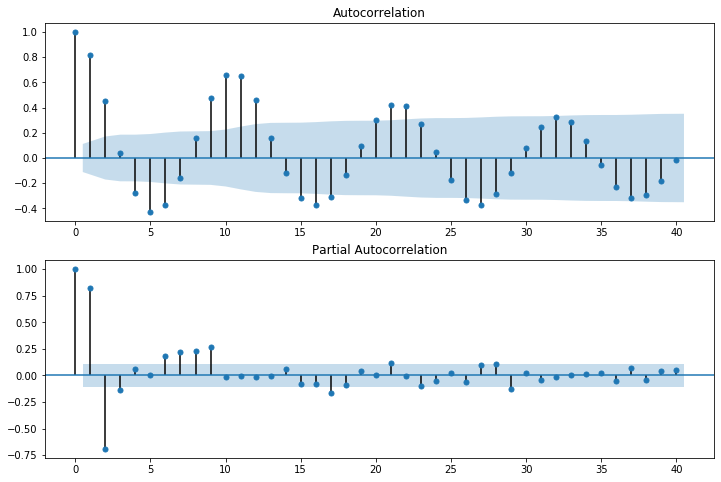
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(dta.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(dta, lags=40, ax=ax2)
[9]:
arma_mod20 = sm.tsa.ARMA(dta, (2,0)).fit(disp=False)
print(arma_mod20.params)
const 49.659415
ar.L1.SUNACTIVITY 1.390656
ar.L2.SUNACTIVITY -0.688571
dtype: float64
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/base/tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
% freq, ValueWarning)
[10]:
arma_mod30 = sm.tsa.ARMA(dta, (3,0)).fit(disp=False)
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/base/tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
% freq, ValueWarning)
[11]:
print(arma_mod20.aic, arma_mod20.bic, arma_mod20.hqic)
2622.636338063735 2637.5697031713257 2628.606725908981
[12]:
print(arma_mod30.params)
const 49.749907
ar.L1.SUNACTIVITY 1.300810
ar.L2.SUNACTIVITY -0.508093
ar.L3.SUNACTIVITY -0.129650
dtype: float64
[13]:
print(arma_mod30.aic, arma_mod30.bic, arma_mod30.hqic)
2619.403628696615 2638.070335081104 2626.8666135031726
Does our model obey the theory?
[14]:
sm.stats.durbin_watson(arma_mod30.resid.values)
[14]:
1.9564809883560828
[15]:
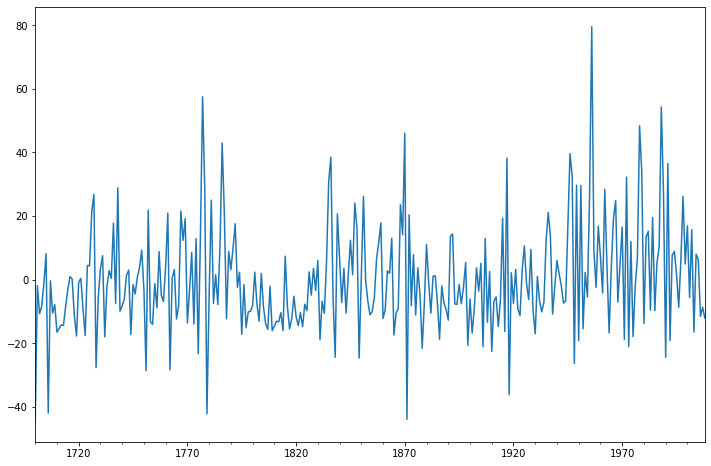
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
ax = arma_mod30.resid.plot(ax=ax);
[16]:
resid = arma_mod30.resid
[17]:
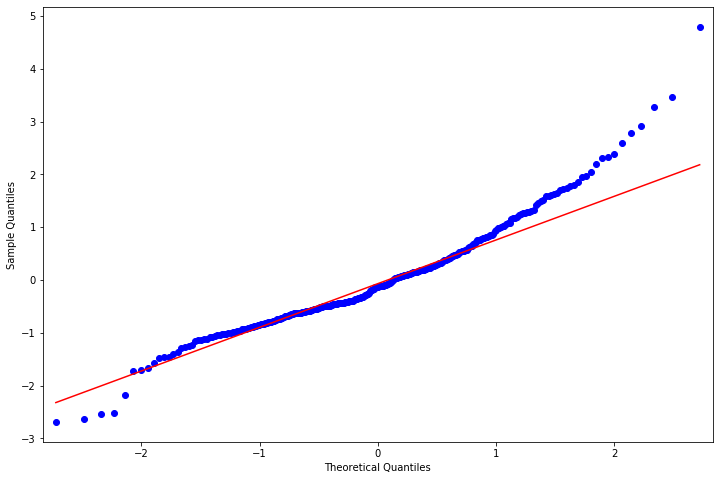
stats.normaltest(resid)
[17]:
NormaltestResult(statistic=49.84501653358502, pvalue=1.500694132607906e-11)
[18]:
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q', ax=ax, fit=True)
[19]:
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)
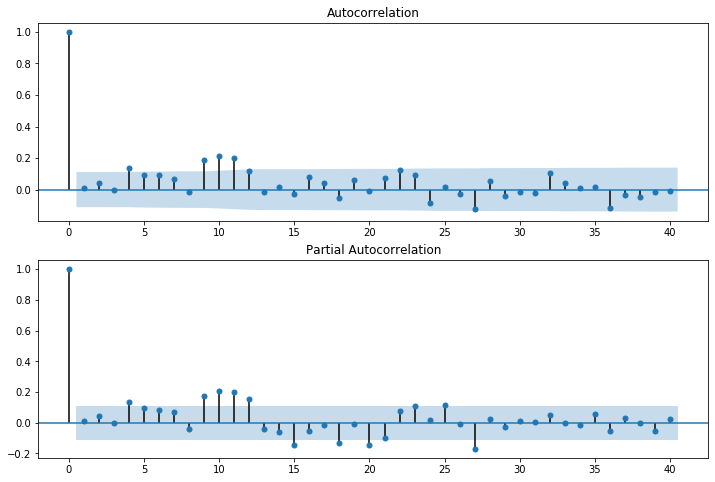
[20]:
r,q,p = sm.tsa.acf(resid.values.squeeze(), fft=True, qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))
AC Q Prob(>Q)
lag
1.0 0.009179 0.026286 8.712037e-01
2.0 0.041793 0.573042 7.508715e-01
3.0 -0.001335 0.573601 9.024483e-01
4.0 0.136089 6.408924 1.706201e-01
5.0 0.092468 9.111835 1.046857e-01
6.0 0.091948 11.793251 6.674327e-02
7.0 0.068748 13.297210 6.518964e-02
8.0 -0.015020 13.369238 9.976106e-02
9.0 0.187592 24.641917 3.393901e-03
10.0 0.213718 39.321999 2.229470e-05
11.0 0.201082 52.361140 2.344947e-07
12.0 0.117182 56.804191 8.574250e-08
13.0 -0.014055 56.868327 1.893901e-07
14.0 0.015398 56.945567 3.997654e-07
15.0 -0.024967 57.149321 7.741463e-07
16.0 0.080916 59.296773 6.872153e-07
17.0 0.041138 59.853743 1.110942e-06
18.0 -0.052021 60.747433 1.548429e-06
19.0 0.062496 62.041696 1.831640e-06
20.0 -0.010301 62.076984 3.381236e-06
21.0 0.074453 63.926657 3.193581e-06
22.0 0.124955 69.154773 8.978346e-07
23.0 0.093162 72.071036 5.799778e-07
24.0 -0.082152 74.346689 4.713012e-07
25.0 0.015695 74.430045 8.289034e-07
26.0 -0.025037 74.642903 1.367283e-06
27.0 -0.125861 80.041147 3.722566e-07
28.0 0.053225 81.009981 4.716277e-07
29.0 -0.038693 81.523807 6.916630e-07
30.0 -0.016904 81.622226 1.151661e-06
31.0 -0.019296 81.750939 1.868765e-06
32.0 0.104990 85.575064 8.927958e-07
33.0 0.040086 86.134565 1.247509e-06
34.0 0.008829 86.161808 2.047826e-06
35.0 0.014588 86.236445 3.263808e-06
36.0 -0.119329 91.248895 1.084455e-06
37.0 -0.036665 91.723863 1.521924e-06
38.0 -0.046193 92.480511 1.938736e-06
39.0 -0.017768 92.592880 2.990681e-06
40.0 -0.006220 92.606703 4.696987e-06
This indicates a lack of fit.
In-sample dynamic prediction. How good does our model do?
[21]:
predict_sunspots = arma_mod30.predict('1990', '2012', dynamic=True)
print(predict_sunspots)
1990-12-31 167.047407
1991-12-31 140.992977
1992-12-31 94.859076
1993-12-31 46.860856
1994-12-31 11.242539
1995-12-31 -4.721335
1996-12-31 -1.166946
1997-12-31 16.185664
1998-12-31 39.021861
1999-12-31 59.449852
2000-12-31 72.170122
2001-12-31 75.376759
2002-12-31 70.436428
2003-12-31 60.731551
2004-12-31 50.201759
2005-12-31 42.075989
2006-12-31 38.114251
2007-12-31 38.454610
2008-12-31 41.963785
2009-12-31 46.869258
2010-12-31 51.423232
2011-12-31 54.399689
2012-12-31 55.321659
Freq: A-DEC, dtype: float64
[22]:
fig, ax = plt.subplots(figsize=(12, 8))
ax = dta.loc['1950':].plot(ax=ax)
fig = arma_mod30.plot_predict('1990', '2012', dynamic=True, ax=ax, plot_insample=False)
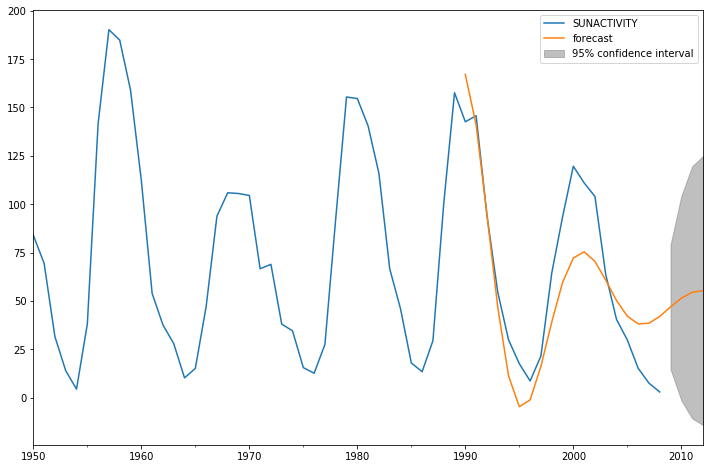
[23]:
def mean_forecast_err(y, yhat):
return y.sub(yhat).mean()
[24]:
mean_forecast_err(dta.SUNACTIVITY, predict_sunspots)
[24]:
5.63698929359919
Exercise: Can you obtain a better fit for the Sunspots model? (Hint: sm.tsa.AR has a method select_order)¶
Simulated ARMA(4,1): Model Identification is Difficult¶
[25]:
from statsmodels.tsa.arima_process import ArmaProcess
[26]:
np.random.seed(1234)
# include zero-th lag
arparams = np.array([1, .75, -.65, -.55, .9])
maparams = np.array([1, .65])
Let’s make sure this model is estimable.
[27]:
arma_t = ArmaProcess(arparams, maparams)
[28]:
arma_t.isinvertible
[28]:
True
[29]:
arma_t.isstationary
[29]:
False
What does this mean?
[30]:
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
ax.plot(arma_t.generate_sample(nsample=50));
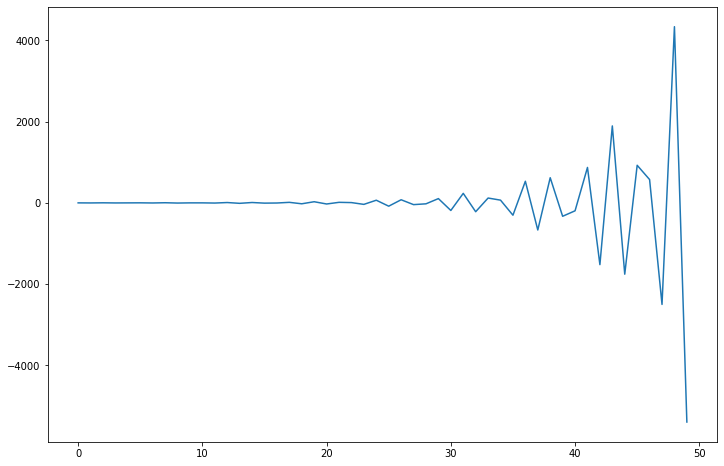
[31]:
arparams = np.array([1, .35, -.15, .55, .1])
maparams = np.array([1, .65])
arma_t = ArmaProcess(arparams, maparams)
arma_t.isstationary
[31]:
True
[32]:
arma_rvs = arma_t.generate_sample(nsample=500, burnin=250, scale=2.5)
[33]:
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(arma_rvs, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(arma_rvs, lags=40, ax=ax2)
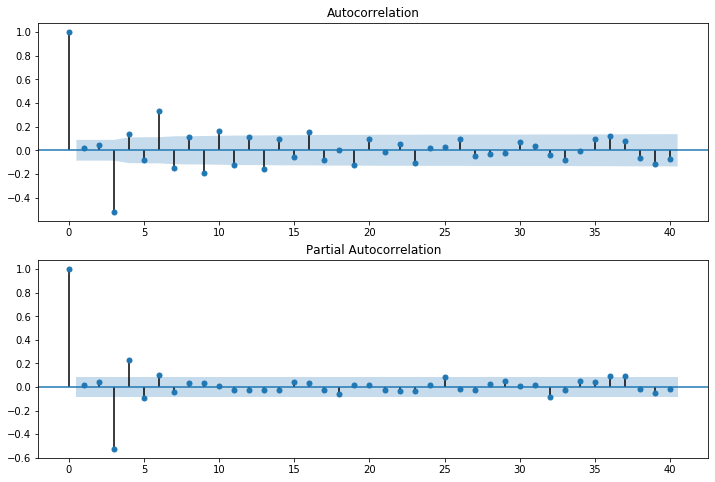
For mixed ARMA processes the Autocorrelation function is a mixture of exponentials and damped sine waves after (q-p) lags.
The partial autocorrelation function is a mixture of exponentials and dampened sine waves after (p-q) lags.
[34]:
arma11 = sm.tsa.ARMA(arma_rvs, (1,1)).fit(disp=False)
resid = arma11.resid
r,q,p = sm.tsa.acf(resid, fft=True, qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))
AC Q Prob(>Q)
lag
1.0 0.254921 32.687652 1.082226e-08
2.0 -0.172416 47.670706 4.450797e-11
3.0 -0.420945 137.159366 1.548487e-29
4.0 -0.046875 138.271272 6.617800e-29
5.0 0.103240 143.675871 2.958774e-29
6.0 0.214864 167.132969 1.823745e-33
7.0 -0.000889 167.133371 1.009220e-32
8.0 -0.045418 168.185721 3.094882e-32
9.0 -0.061445 170.115773 5.837297e-32
10.0 0.034623 170.729827 1.958763e-31
11.0 0.006351 170.750528 8.267165e-31
12.0 -0.012882 170.835880 3.220277e-30
13.0 -0.053959 172.336519 6.181277e-30
14.0 -0.016606 172.478936 2.160243e-29
15.0 0.051742 173.864458 4.089601e-29
16.0 0.078917 177.094252 3.217978e-29
17.0 -0.001834 177.096000 1.093182e-28
18.0 -0.101604 182.471907 3.103866e-29
19.0 -0.057342 184.187742 4.624129e-29
20.0 0.026975 184.568256 1.235687e-28
21.0 0.062359 186.605932 1.530280e-28
22.0 -0.009400 186.652334 4.548257e-28
23.0 -0.068037 189.088154 4.562074e-28
24.0 -0.035566 189.755170 9.901231e-28
25.0 0.095679 194.592591 3.354336e-28
26.0 0.065650 196.874845 3.487671e-28
27.0 -0.018404 197.054581 9.008875e-28
28.0 -0.079244 200.393976 5.773794e-28
29.0 0.008499 200.432469 1.541408e-27
30.0 0.053372 201.953742 2.133223e-27
31.0 0.074816 204.949362 1.550183e-27
32.0 -0.071187 207.667209 1.262306e-27
33.0 -0.088145 211.843121 5.480895e-28
34.0 -0.025283 212.187415 1.215245e-27
35.0 0.125690 220.714864 8.231729e-29
36.0 0.142724 231.734081 1.923112e-30
37.0 0.095768 236.706123 5.937874e-31
38.0 -0.084744 240.607766 2.890931e-31
39.0 -0.150126 252.878943 3.963067e-33
40.0 -0.083767 256.707701 1.996205e-33
[35]:
arma41 = sm.tsa.ARMA(arma_rvs, (4,1)).fit(disp=False)
resid = arma41.resid
r,q,p = sm.tsa.acf(resid, fft=True, qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))
AC Q Prob(>Q)
lag
1.0 -0.007889 0.031302 0.859569
2.0 0.004132 0.039907 0.980244
3.0 0.018103 0.205416 0.976710
4.0 -0.006760 0.228539 0.993948
5.0 0.018120 0.395025 0.995466
6.0 0.050688 1.700448 0.945087
7.0 0.010252 1.753955 0.972196
8.0 -0.011206 1.818018 0.986092
9.0 0.020292 2.028518 0.991009
10.0 0.001029 2.029060 0.996113
11.0 -0.014035 2.130168 0.997984
12.0 -0.023858 2.422925 0.998427
13.0 -0.002108 2.425216 0.999339
14.0 -0.018783 2.607429 0.999590
15.0 0.011316 2.673698 0.999805
16.0 0.042159 3.595419 0.999443
17.0 0.007943 3.628204 0.999734
18.0 -0.074311 6.503854 0.993686
19.0 -0.023379 6.789066 0.995256
20.0 0.002398 6.792072 0.997313
21.0 0.000487 6.792197 0.998516
22.0 0.017952 6.961434 0.999024
23.0 -0.038576 7.744465 0.998744
24.0 -0.029816 8.213248 0.998859
25.0 0.077850 11.415822 0.990675
26.0 0.040408 12.280446 0.989479
27.0 -0.018612 12.464273 0.992262
28.0 -0.014764 12.580184 0.994586
29.0 0.017650 12.746188 0.996111
30.0 -0.005486 12.762261 0.997504
31.0 0.058256 14.578542 0.994614
32.0 -0.040840 15.473082 0.993887
33.0 -0.019493 15.677307 0.995393
34.0 0.037269 16.425463 0.995214
35.0 0.086212 20.437446 0.976296
36.0 0.041271 21.358844 0.974774
37.0 0.078704 24.716875 0.938948
38.0 -0.029729 25.197052 0.944895
39.0 -0.078397 28.543384 0.891179
40.0 -0.014466 28.657574 0.909268
Exercise: How good of in-sample prediction can you do for another series, say, CPI¶
[36]:
macrodta = sm.datasets.macrodata.load_pandas().data
macrodta.index = pd.Index(sm.tsa.datetools.dates_from_range('1959Q1', '2009Q3'))
cpi = macrodta["cpi"]
Hint:¶
[37]:
fig = plt.figure(figsize=(12,8))
ax = fig.add_subplot(111)
ax = cpi.plot(ax=ax);
ax.legend();
P-value of the unit-root test, resoundingly rejects the null of a unit-root.
[38]:
print(sm.tsa.adfuller(cpi)[1])
0.9904328188337421