Autoregressive Moving Average (ARMA): Sunspots data¶

This notebook replicates the existing ARMA notebook using the statsmodels.tsa.statespace.SARIMAX class rather than the statsmodels.tsa.ARMA class.

[1]:

%matplotlib inline

[2]:

import numpy as np
from scipy import stats
import pandas as pd
import matplotlib.pyplot as plt

import statsmodels.api as sm

[3]:

from statsmodels.graphics.api import qqplot

Sunspots Data¶

[4]:

print(sm.datasets.sunspots.NOTE)

::

    Number of Observations - 309 (Annual 1700 - 2008)
    Number of Variables - 1
    Variable name definitions::

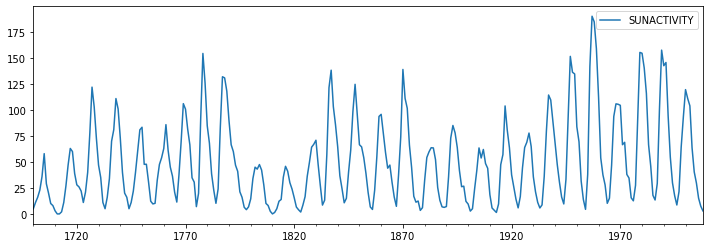
        SUNACTIVITY - Number of sunspots for each year

    The data file contains a 'YEAR' variable that is not returned by load.

[5]:

dta = sm.datasets.sunspots.load_pandas().data

[6]:

dta.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008'))
del dta["YEAR"]

[7]:

dta.plot(figsize=(12,4));

../../../_images/examples_notebooks_generated_statespace_arma_0_9_0.png

[8]:

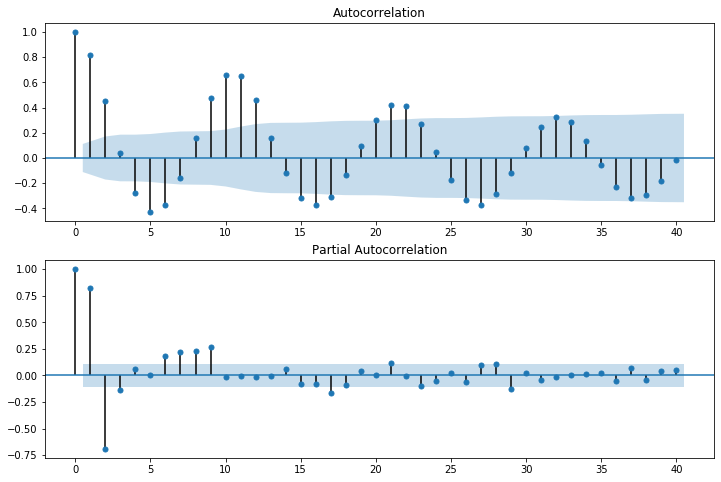
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(dta.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(dta, lags=40, ax=ax2)

../../../_images/examples_notebooks_generated_statespace_arma_0_10_0.png

[9]:

arma_mod20 = sm.tsa.statespace.SARIMAX(dta, order=(2,0,0), trend='c').fit(disp=False)
print(arma_mod20.params)

/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/base/tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
  % freq, ValueWarning)
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/base/tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
  % freq, ValueWarning)

intercept     14.793947
ar.L1          1.390659
ar.L2         -0.688568
sigma2       274.761104
dtype: float64

[10]:

arma_mod30 = sm.tsa.statespace.SARIMAX(dta, order=(3,0,0), trend='c').fit(disp=False)

/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/base/tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
  % freq, ValueWarning)
/home/travis/build/statsmodels/statsmodels/statsmodels/tsa/base/tsa_model.py:162: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used.
  % freq, ValueWarning)

[11]:

print(arma_mod20.aic, arma_mod20.bic, arma_mod20.hqic)

2622.6363381415617 2637.5697032491526 2628.6067259868078

[12]:

print(arma_mod30.params)

intercept     16.762205
ar.L1          1.300810
ar.L2         -0.508122
ar.L3         -0.129612
sigma2       270.102651
dtype: float64

[13]:

print(arma_mod30.aic, arma_mod30.bic, arma_mod30.hqic)

2619.4036296635877 2638.0703360480766 2626.866614470145

Does our model obey the theory?

[14]:

sm.stats.durbin_watson(arma_mod30.resid)

[14]:

1.9564844832075043

[15]:

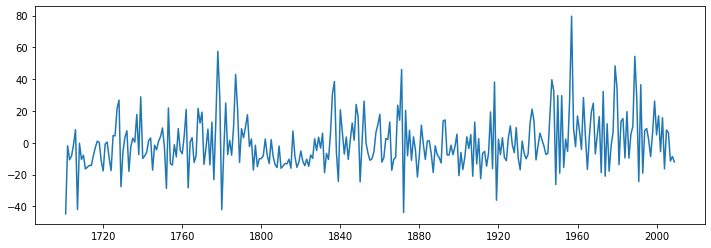
fig = plt.figure(figsize=(12,4))
ax = fig.add_subplot(111)
ax = plt.plot(arma_mod30.resid)

../../../_images/examples_notebooks_generated_statespace_arma_0_18_0.png

[16]:

resid = arma_mod30.resid

[17]:

stats.normaltest(resid)

[17]:

NormaltestResult(statistic=49.84700651506573, pvalue=1.4992016984440667e-11)

[18]:

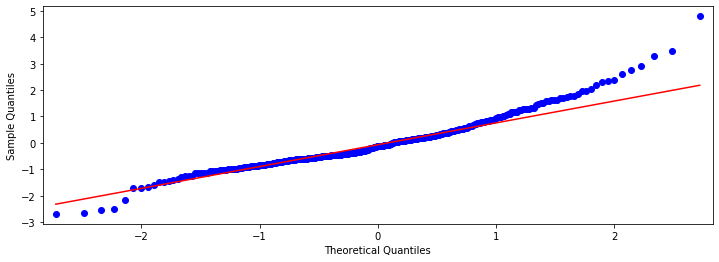
fig = plt.figure(figsize=(12,4))
ax = fig.add_subplot(111)
fig = qqplot(resid, line='q', ax=ax, fit=True)

../../../_images/examples_notebooks_generated_statespace_arma_0_21_0.png

[19]:

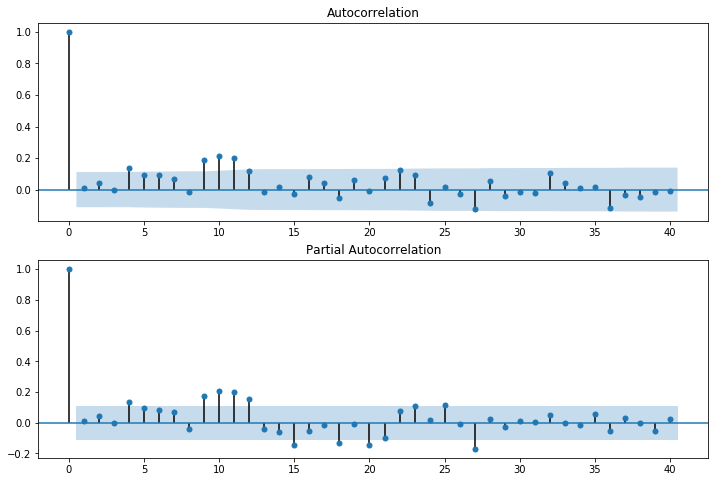
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid, lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)

../../../_images/examples_notebooks_generated_statespace_arma_0_22_0.png

[20]:

r,q,p = sm.tsa.acf(resid, fft=True, qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))

            AC          Q      Prob(>Q)
lag
1.0   0.009176   0.026273  8.712350e-01
2.0   0.041820   0.573727  7.506142e-01
3.0  -0.001342   0.574292  9.022915e-01
4.0   0.136064   6.407488  1.707135e-01
5.0   0.092433   9.108334  1.048203e-01
6.0   0.091919  11.788017  6.686844e-02
7.0   0.068735  13.291374  6.531943e-02
8.0  -0.015021  13.363410  9.994251e-02
9.0   0.187599  24.636915  3.400198e-03
10.0  0.213724  39.317880  2.233182e-05
11.0  0.201092  52.358270  2.347759e-07
12.0  0.117192  56.802109  8.581667e-08
13.0 -0.014051  56.866210  1.895534e-07
14.0  0.015394  56.943403  4.001106e-07
15.0 -0.024986  57.147464  7.747085e-07
16.0  0.080892  59.293626  6.880521e-07
17.0  0.041120  59.850085  1.112486e-06
18.0 -0.052030  60.744064  1.550379e-06
19.0  0.062500  62.038494  1.833802e-06
20.0 -0.010292  62.073718  3.385224e-06
21.0  0.074467  63.924062  3.196544e-06
22.0  0.124962  69.152771  8.984834e-07
23.0  0.093170  72.069532  5.802915e-07
24.0 -0.082149  74.345041  4.715787e-07
25.0  0.015689  74.428332  8.294020e-07
26.0 -0.025049  74.641400  1.367992e-06
27.0 -0.125875  80.040873  3.722921e-07
28.0  0.053215  81.009318  4.717356e-07
29.0 -0.038699  81.523324  6.917767e-07
30.0 -0.016896  81.621648  1.151883e-06
31.0 -0.019286  81.750227  1.869202e-06
32.0  0.105001  85.575148  8.927709e-07
33.0  0.040094  86.134872  1.247384e-06
34.0  0.008834  86.162142  2.047606e-06
35.0  0.014588  86.236784  3.263459e-06
36.0 -0.119334  91.249666  1.084187e-06
37.0 -0.036673  91.724838  1.521456e-06
38.0 -0.046204  92.481862  1.937920e-06
39.0 -0.017775  92.594310  2.989369e-06
40.0 -0.006219  92.608126  4.694971e-06

This indicates a lack of fit.
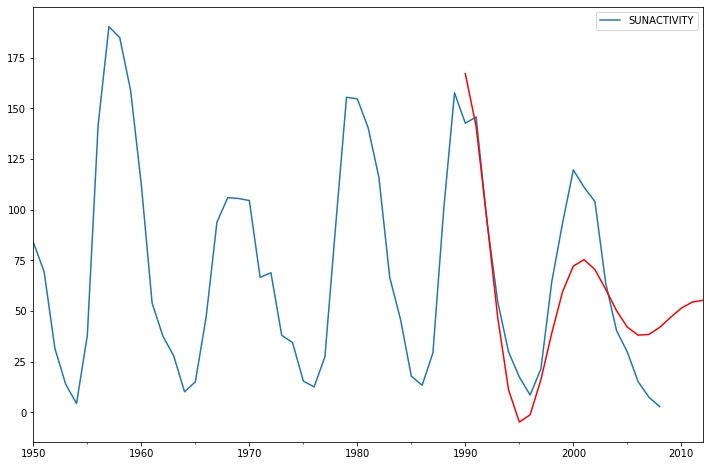
In-sample dynamic prediction. How good does our model do?

[21]:

predict_sunspots = arma_mod30.predict(start='1990', end='2012', dynamic=True)

[22]:

fig, ax = plt.subplots(figsize=(12, 8))
dta.loc['1950':].plot(ax=ax)
predict_sunspots.plot(ax=ax, style='r');

../../../_images/examples_notebooks_generated_statespace_arma_0_27_0.png

[23]:

def mean_forecast_err(y, yhat):
    return y.sub(yhat).mean()

[24]:

mean_forecast_err(dta.SUNACTIVITY, predict_sunspots)

[24]:

5.635549823472533